اقتراحات مكتبة منصات
       

INTRODUCTION

 
INTRODUCTION

Les Mathématiques constituent une activité de l'esprit qui prend les dimensions d'une grande aventure humaine. Elles sont un champ fertile au développement de la pensée critique, à la formation de l'habitude à l'honnêteté scientifique, à l'objectivité, à la rigueur et à la précision. Elles offrent aux élèves des connaissances nécessaires à la vie sociale et des moyens efficaces pour comprendre et explorer le monde réel quel qu'en soit le domaine : physique, chimique, biologique, astronomique, social, psychologique, informatique, etc....

L'avancement fulgurant des sciences et des technologies a profondément marqué la société moderne. On parle aujourd'hui de l'ère de l'«information» comme on parlait, il y a un quart de siècle, de l'ère industrielle. Or, tout le monde est d'accord sur le fait que ce développement n'a pu s'accomplir que grâce à l'outil mathématique dont l'emploi a permis de substituer à la description qualitative du réel, sa quantification et sa modélisation opérationnelle. Aujourd'hui, plus que jamais, les Mathématiques s'avèrent être d'une nécessité inéluctable à la vie des sociétés et à leur développement. Cette science ne peut plus rester l'apanage d'une élite spécialisée, mais beaucoup de ses résultats et moyens doivent être acquis par un nombre de citoyens de plus en plus considérable.

Cette extension des Mathématiques à tout le réel, et la demande accrue pour son apprentissage, en ont, sans doute, modifié l'esprit et l'usage. La réforme de leur enseignement est à opérer dans trois axes : une nouvelle formulation des objectifs, une refonte des contenus et un choix convenable des méthodes.

Formulation des objectifs: Les objectifs fondamentaux concernant les activités mentales ainsi que la formation au raisonnement mathématique, continuent à figurer au programme, l'accent étant surtout mis sur la construction individuelle des Mathématiques, il ne s'agit plus d'apprendre des Mathématiques toutes faites mais de les faire par soi-même. A partir de situations réelles dans lesquelles les élèves soulèvent des questions, posent des problèmes, formulent des hypothèses et les vérifient, l'esprit même de cette science s'implante et s'enracine.

Notre intention est aussi de former les élèves à la communication: lire un texte mathématique, le comprendre, l'interpréter, utiliser des symboles, des graphiques, des tableaux etc..., rédiger une démonstration, expliquer une situation etc...restent des objectifs essentiels de l'enseignement.

Refonte des contenus: Les sujets traités ne sont pas jugés d'après leur intérêt théorique mais pratique. Ils doivent être accessibles à tous les élèves et répondre à leur besoin de formation et à leur développement culturel. Tout abus théorique fut aboli; toute virtuosité dans l'accomplissement des tâches fut omise. Ceci a permis un allègement significatif des programmes qui cherchent à former des "têtes bien faites". L'introduction de la machine à calculer et la possibilité d'utiliser l'ordinateur sont deux nouveautés technologiques qui auront des bienfaits sur la formation. D'autres sujets concernant le traitement de l'information, comme les Statistiques, permettent une meilleure adaptation des nouvelles générations aux problèmes socio-économiques.
Méthode d'enseignement : L'enseignement des Mathématiques doit s'organiser de façon à les démythifier et à les rendre accessibles à un large public. La méthode préconisée consiste à partir de situations réelles, vécues ou familières pour montrer qu'il n'y a pas de divorce entre les Mathématiques et la vie quotidienne. Cette pratique des Mathématiques amènera l'élève à l'intelligence des modèles conceptuels dont il comprendra l'efficacité grâce au transfert des apprentissages réussis.

Tel fut le contexte dans lequel ce nouveau programme a été préparé. Notre but essentiel est de former un citoyen à part entière capable de réflexion critique et d'autonomie intellectuelle.

 
OBJECTIFS GENERAUX

Le présent curriculum se propose de réaliser, à travers l'acquisition d'un savoir mathématique adéquat, les objectifs généraux suivants :

La formation à la construction d'arguments et à leur évaluation, le développement de la pensée critique, la formation au RAISONNEMENT MATHEMATIQUE sont des intentions majeures de ce curriculum. Pour cela l'occasion doit être toujours offerte aux élèves pour :

Observer, analyser, abstraire, douter, prévoir, conjecturer, généraliser, synthétiser, interpréter, démontrer.

La RESOLUTION DE PROBLEMES est peut-être l'activité la plus significative dans l'enseignement des mathématiques. D'une part tout savoir mathématique nouveau doit être construit à partir de situations-problèmes. D'autre part, l'élève doit apprendre à utiliser différentes stratégies pour surmonter les difficultés et arriver à résoudre un problème. Pour cela il doit être capable de :

Sérier, classifier, quantifier, retrouver des modèles mathématiques, manier des techniques de simulation, construire et utiliser des algorithmes, prendre des décisions, vérifier, appliquer, mesurer, employer des techniques heuristiques, traiter des informations.

La société moderne a de plus en plus besoin de main-d'œvre hautement qualifiée et de chercheurs dans tous les domaines. Le curriculum de Mathématiques répond à ces exigences en offrant à l'élève l'occasion de :

Pratiquer une démarche scientifique, développer l'esprit scientifique, s'initier à la recherche, établir des relations entre les mathématiques et la réalité environnante dans toutes ses dimensions, valoriser le rôle des Mathématiques dans le développement technologique, économique et culturel.

Notre intention est de former l'élève à la COMMUNICATION MATHEMATIQUE. Pour cela il doit être entraîné à :
Coder et décoder des messages, formuler, exprimer oralement, par écrit et/ou à l'aide d'outils mathématiques des informations diverses.
Bien qu'elles soient une science utilitaire, les Mathématiques sont aussi un art. Le curriculum offre à l'élève l'occasion de les VALORISER en l'aidant à :

Acquérir la confiance dans la méthode mathématique, valoriser la rigueur et la précision, apprécier l'ordre et l'harmonie interne des théories mathématiques, développer son intuition, son imagination et sa créativité, prendre plaisir dans les activités intellectuelles, persévérer au travail.

 
REPARTITION HEBDOMADAIRE ET ANNUELLE DES PERIODES

Niveau

Enseignement de Base

Enseignement Secondaire

 Primaire

Moyen

Cycle

1er Cycle

2ème Cycle

 

1ère

2ème Année

3ème Année

Année Scolaire

1ère

2ème

3ème

4ème

5ème

6ème

7ème

8ème

9ème

Année

Humanités

Sciences

Lettres

et Humanités

Sociologie

et Economie

Sciences

Générales

Sciences

de la Vie

Périodes Hebdomadaires

 

5

5

5

5

5

5

5

5

5

5

4

6

2

4

10

5

Périodes Annuelles

 

150

150

150

150

150

150

150

150

150

150

120

180

60

120

300

150

 

EDUCATION DE BASE

 
PROGRESSION DU CONTENU - PREMIER CYCLE

 

ARITHMETIQUE  ET  ALGEBRE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. NOMBRES

 

 

 
  • ENTIERS NATURELS (60 h)
  • Nombres inférieurs à 100.
  • Lecture, écriture en chiffres.
  • Comparaison.
  • Groupement par 10.

 
  • ENTIERS NATURELS (60 h)
  • Nombres inférieurs à 100.
  • Lecture, écriture en chiffres.
  • Comparaison.
  • Groupement par 10.

 
  • ENTIERS NATURELS (25 h)
  • Nombres inférieurs à 1 000.
  • Lecture et écriture en lettres des nombres inférieurs à 100.
  • Ordre; signes < et >; représentation sur une droite.
  • Ecriture développée.

 

2. OPERATIONS
  • ADDITION (50 h)
  • Addition des entiers.
  • Fonction "ajouter n".
  • Tables d'addition: construction (jusqu'à 9).
  • Technique opératoire avec retenue.
  • Décomposition d'un entier.

 

  • SOUSTRACTION (10 h)
  • Initiation.
  •  ADDITION (50 h)
  • Addition des entiers.
  • Fonction "ajouter n".
  • Tables d'addition: construction (jusqu'à 9).
  • Technique opératoire avec retenue.
  • Décomposition d'un entier.

 

  •  SOUSTRACTION (10 h)
  • Initiation.
  • ADDITION (30 h)
  • Mémorisation des tables d'addition.
  • Maîtrise de la technique opératoire.

 

  • SOUSTRACTION (30 h)
  • Opération inverse de l'addition.
  • Fonction "soustraire n".
  • Technique opératoire: emprunt à l'unité contiguë.

 

  • MULTIPLICATION (30 h)
  • Addition itérative.
  • Table de multiplication: construction (jusqu'à 9).
  • Multiplication par un nombre à un chiffre.

 

  • DIVISION (5 h)
  • Initiation: partage, distribution.

 
 

 

 

GEOMETRIE 
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. LOCALISATION ET

    REPERAGE
  • Domaine.
  • Déplacement.
  • Positionnementdans l'espace.
  • Repérage d'un point.

 

 
  • Milieu d'un segment de droite.
  • Droites perpendiculaires.

 

 

(10 h)

(5 h)

(5 h)

2. CORPS SOLIDES
  • Pavé. Cube. Sphère. Cylindre. Cône. 

 
  • Description de solides: sommets, arêtes et faces.
  • Construction d'un cube et d'un pavé.

 

 

(5 h)

(5 h)

(7 h)

3. FIGURES PLANES
  • Lignes.
  • Carré. Rectangle. Triangle. Disque.

 
  • Segment de droite.
  • Description de figures planes: sommets et côtés. 
  • Angle droit. Application au rectangle et au carré.

 

 

(5 h)

(5 h)

(3 h)

4. TRANSFORMATIONS
  • Axe de symétrie.   
  • Figures ayant un axe de symétrie.
  • Réflexion.             

 

(5 h)

(5 h)

(5 h)
 

 

 

MESURE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. LONGUEUR
  • Comparaison de longueurs.     

 

 

 

 
  • Mesure de longueurs: le mètre, le centimètre.

 

 

 
  • Unités de longueur: kilomètre, mètre, centimètre, millimètre.
  • Distance entre deux points.
  • Longueur d'une ligne polygonale. Périmètre.

 

(5 h)

(5 h)

(10 h)

2. MASSE

 
  • Comparaison de masses.
  • Kilogramme. Gramme.

 

 

(5 h)

(5 h)

3. TEMPS ET DUREE

 

 
  • Lecture de l'heure.
  • Durée d'un événement.
  • Unités de temps: heure, minute, seconde.

 

 

 

(5 h)
 

 

 
PROGRESSION DU CONTENU - SECOND CYCLE

 

ARITHMETIQUE  ET  ALGEBRE
 

 

Classe

4ème année

5ème année

6ème année

Sujet

 

 

 

1. NOMBRES

 
  • ENTIERS NATURELS (15 h)
  • Nombres supérieurs à 100 000.
  • Multiples d'un entier.
  • Critères de divisibilité par 2, 5 et 10.
  • Numération sexagésimale.

 

  • FRACTIONS (15 h)
  • Fractions  ( a £ b).
  • Comparaison de fractions.

 

  • DECIMAUX (10 h)
  • Nombres décimaux.
  • ENTIERS NATURELS (20 h)
  • Critères de divisibilité par 3, 4 et 9.
  • Multiples communs de deux entiers.
  • Diviseurs d'un entier.
  • Diviseurs communs de deux entiers.
  • Système de numération décimale.

 

  • FRACTIONS (10 h)   
  • Egalité et simplification des fractions.
  • Nombres mixtes.

 

  • DECIMAUX (10 h)
  • Comparaison et représentation des nombres décimaux.
  • ENTIERS NATURELS (15 h)
  • Développement d'un entier naturel selon les
    puissances de 10.
  • P.G.C.D et P.P.C.M de deux entiers naturels.
  • Nombres premiers entre eux.

 

  • FRACTIONS (10 h)
  • Fractions irréductibles.   
  • Fractions décimales.

 

  • DECIMAUX (10 h)
  • Ecriture fractionnaire d'un nombre décimal.
  • Développement d'un nombre décimal selon les puissances de 10 et de .

 

  • NOMBRES RELATIFS (15 h)
  • Nombres positifs et nombres négatifs.   
  • Représentation sur l'axe numérique.
  • Comparaison.

2. OPERATIONS
  • ADDITION (15 h)
  • Addition des décimaux.
  • Addition des fractions de même dénominateur.
  • Addition de durées et de temps.

 

  • SOUSTRACTION (15 h)
  • Soustraction de décimaux.
  • Soustraction de fractions de même dénominateur.
  • Soustraction de durées et de temps.

 

  • MULTIPLICATION (10 h)
  • Multiplication d'un décimal par un entier.
  • Propriétés: la commutativité et l'associativité.
  • Distributivité de la multiplication par rapport à l'addition et à la soustraction.

 

  • DIVISION (30 h)
  • Technique opératoire sur les entiers: diviseurs à deux.
  • chiffres au plus, quotient entier.
  • Fonction "diviser par n".
  • ADDITION (15 h)
  • Addition de fractions.
  • Addition de décimaux à plusieurs décimales.

 

  • SOUSTRACTION (15 h)
  • Soustraction de fractions.
  • Soustraction de décimaux à plusieurs décimales.

   

  • MULTIPLICATION (20 h)
  • Multiplication de décimaux.
  • Fonction "multiplier par ".
  • Produit d'une durée par un entier.

 

  • DIVISION (10 h)
  • Quotient décimal d'une division.

 

 
  • ADDITION (5 h)
  • Addition de nombres relatifs.

 

  • SOUSTRACTION (5 h)
  • Soustraction de nombres relatifs.

 

  • MULTIPLICATION (10 h)
  • Multiplication de fractions.
  • Puissances d'exposant 2 et 3.               Puissances de 10.

 

  • DIVISION (10 h)
  • Division de fractions.
  • Quotient et rapport.
  • Division d'une durée par un entier.

3. PROPORTIONNALITE

 

 
  • Pourcentage. Taux.
  • Suites proportionnelles.
  • Echelle.                                                  

 

 

 

(20 h)

4.  EXPRESSION

    ALGEBRIQUE

 

 
  • Lois de priorités des opérations dans un calcul.
  • Calcul sur les expressions littérales.
  • Valeur numérique d'une expression littérale.                                                                              

 

 

 

(10 h)
 

 

 

GEOMETRIE 
 

 

Classe

4ème année

5ème année

6ème année

Sujet

 

 

 

1. LOCALISATION ET REPERAGE   
  • Distance d'un point à une droite. 
  • Localisation d'un point sur un quadrillage.
  • Distance de deux droites parallèles.

 

 

 
  • Positions relatives de deux droites dans un plan.
  • Positions relatives d'une droite et d'un cercle.

 

(5 h)

(3 h)

(2 h)

2. CORPS SOLIDES
  • Construction de solides.
  • Développement de solides.
  • Patrons de solides.                                                                      

 

(5 h)

(7 h)

(3 h)

3. FIGURES PLANES
  • Droites concourantes. Droites parallèles.
  • Classification des quadrilatères selon leurs côtés.       
  • Cercle. Disque. 

 

 
  • Angle.
  • Diagonales d'un polygone.
  • Classification des quadrilatères selon les diagonales.
  • Diamètre d'un cercle.

 
  • Angles adjacents, angles opposés par le sommet.
  • Bissectrice d'un angle.
  • Médiatrice d'un segment de droite.
  • Triangle: triangles particuliers; droites particulières dans un  triangle; somme des angles d'un triangle.                        

 

(5 h)

(10 h)

(10 h)

4. TRANSFORMATIONS
  • Dessin du symétrique d'une figure par rapport à un axe.
  • Homothétie.

 
  • Symétrie centrale.
  • Etude de figures à partir de leurs éléments de symétrie.        

 

(5 h)

(5 h)

(10 h)
 

 

 

MESURE
 

 

Classe

4ème année

5ème année

6ème année

Sujet

 

 

 

1. LONGUEUR  
  • Système métrique des unités de longueur.           
  • Longueur d'un cercle.              

 

 

(6 h)

(3 h)

 

2. MASSE
  • Système métrique des unités de masse.

 

 

 

(3 h)

 

 

3. SURFACE
  • Comparaison d'aires.
  • Aire du carré, rectangle, triangle rectangle, disque.
  • Aire d'un parallélogramme, d'un triangle.
  • Système métrique des unités d'aire.

 

(3 h)

(10 h)

(8 h)

4. ANGLE

 
  • Mesure d'un angle en degré.
  • Angles complémentaires; angles supplémentaires.                   

 

 

(2 h)

(2 h)

5. CAPACITE
  • Litre et sous-multiples.
  • Système métrique des unités de capacité.

 

 

(3 h)

(5 h)

 

6. VOLUME

 

 
  • Calcul de volume: cube, parallélépipède rectangle, cylindre droit, boule.
  • Système métrique des unités de volume.           

 

 

 

(10 h)
 

 

STATISTIQUE
 

 

Classe

4ème année

5ème année

6ème année

Sujet

 

 

 

GESTION DES DONNEES
  • Collecte et organisation de données.

 
  • Représentation des données en bâtons, bandes et pictogramme.
  • Lecture d'un diagramme circulaire.

 

(5 h)

(5 h)

(5 h)
 

 

 
PROGRESSION DU CONTENU – CYCLE MOYEN

 

ARITHMETIQUE  ET  ALGEBRE
 

 

Classe

7ème année

8ème année

9ème année

Sujet

 

 

 

1. NOMBRES

 
  • ENTIERS NATURELS (10 h)
  • Nombres premiers.
  • Décomposition d'un entier en facteurs premiers.

 

  • FRACTIONS (10 h)
  • Réduction de fractions.

  

  • DECIMAUX (5 h)
  • Ecriture décimale d'une fraction.
  • ENTIERS NATURELS (5 h)
  • P.G.C.D et P.P.C.M de plusieurs entiers.

 

  • FRACTIONS (5 h)
  • Fractions littérales.
  • Fractions composées.

 

  • DECIMAUX (5 h)
  • Compatibilité de l'ordre avec les opérations.

 

  • RACINES CARREES (10 h)
  • Racines carrées d'un nombre positif.

 
  • NOMBRES REELS (5 h)
  • Nombres rationnels et irrationnels.

2. OPERATIONS
  • Soustraction et multiplication de nombres relatifs.
  • Puissances d'exposant entier positif d'un nombre positif.
  • Facteur commun. Factorisation.
  • Puissances d'exposant entier positif d'un nombre relatif.
  • Puissances d'exposant entier négatif de 10.
  • Rendre rationnel le dénominateur d'une fraction.
  • Calcul sur les réels.

 

(30 h)

(5 h)

(10 h)

3. PROPORTIONNALITE
  • Grandeurs directement proportionnelles.
  • Grandeurs inversement proportionnelles.
  • Fonctions linéaires et proportionnalité.

 

(10 h)

(5 h)

(5 h)

4.  EXPRESSION

    ALGEBRIQUE
  • Calcul sur des expressions algébriques.
  • Identités remarquables.
  • Expressions littérales sous forme fractionnaire.
  • Expressions algébriques comprenant de radicaux.
  • Polynôme à une variable.

 

(15 h)

(20 h)

(10 h)

5. EQUATIONS ET

    INEQUATIONS
  • Equations se ramenant à ax = b.
  • Equations du type: (ax + b) (cx + d) = 0.
  • Equations et inéquations du premier degré à une inconnue.
  • Equations du type
  • Systèmes d'équations du premier degré à deux inconnues.
  • Systèmes d'inéquations du premier degré à une inconnue.

 

(10 h)

(15 h)

(40 h)
 

               

GEOMETRIE 
 

 

Classe

7ème année

8ème année

9ème année

Sujet

 

 

 

1.  LOCALISATION ET

     REPERAGE   

  

    

 
  • Lieux géométriques et constructions.
  • Repères orthogonaux et coordonnés d'un point dans un plan.

 

 

 

 

 

 
  • Positions relatives de deux cercles.
  • Lieux géométriques et constructions.
  • Coordonnées du milieu d'un segment de droite.       

 

 

 

 
  • Tangentes et cercles.
  • Lieux géométriques et constructions.
  • Représentation graphique d'une droite.
  • Propriétés analytiques du parallélisme et de l'orthogonalité de deux droites.
  • Longueur d'un segment de droite dans un repère orthonormé.
  • Résolution graphique d'un système d'équations linéaires à deux inconnues.   

 

(10 h)

(15 h)

(35 h)

2.  GEOMETRIE DANS

     L'ESPACE
  • Représentation plane d'un cube, d'un parallélépipède rectangle. 
  • Représentation plane d'un cylindre, d'une pyramide, d'un cône, d'une sphère.
  • Positions relatives de droites et de plans.      
  • Intersection d'une droite et d'un solide usuel.
  • Intersection d'un plan et d'un solide usuel.                                    

 

(5 h)

(10 h)

(5 h)

3.  FIGURES PLANES
  • Cas de superposition des triangles.
  • Angles formés par deux droites parallèles coupées par une sécante.
  • Propriétés caractéristiques de la médiatrice d'un segment.
  • Propriétés caractéristiques de la bissectrice d'un angle.                                              
  • Théorème de Pythagore.
  • Théorème des milieux dans un triangle, dans un trapèze.
  • Propriétés caractéristiques du parallélogramme.
  • Angle au centre d'un cercle, angle inscrit dans un cercle. Aire d'un secteur circulaire.                                      
  • Quadrilatères inscriptibles.
  • Théorème de Thalès.
  • Triangles semblables.

 

 

 

 

(35 h)

(40 h)

(20 h)

4. TRANSFORMATIONS ET

    VECTEURS
  • Translation.
  • Vecteur et translation.
  • Vecteur dans un plan.

 

(5 h)

(5 h)

(5 h)

5. TRIGONOMETRIE

 

 
  • Sinus, cosinus et tangente d'un angle aigu dans un triangle rectangle.

 

 

 

 

(5 h)
 

 

STATISTIQUE
 

 

Classe

7ème année

8ème année

9ème année

Sujet

 

 

 

GESTION DES DONNEES
  • Fréquences relatives.
  • Représentations graphiques des données: diagramme en bâtons, polygone des fréquences.
  • Effectifs et fréquences cumulés.
  • Représentations graphiques des données: diagramme circulaire, polygone des fréquences cumulées.         
  • Série statistique à une variable discrète: différentes représentations.
  • Moyenne et moyenne pondérée.

 

(5 h)

(10 h)

(10 h)
 

 

 

EDUCATION DE BASE - ENSEIGNEMENT PRIMAIRE - PREMIER CYCLE

 
OBJECTIFS

Le curriculum de Mathématiques doit, dans les domaines suivants, rendre les élèves capable de:

A. RAISONNEMENT MATHEMATIQUE

Reconnaître des tendances ou des relations dans des suites de faits simples.
Justifier une réponse.

 

B. RESOLUTION DE PROBLEMES

Prendre des initiatives.
Utiliser des techniques mathématiques appropriées pour résoudre des problèmes de la vie courante.
Utiliser des moyens heuristiques pour trouver un résultat.

 

C. COMMUNICATION

Utiliser des représentations figuratives ou symboliques.
S'exprimer correctement par voie orale ou écrite.
Poser des questions et répondre à des questions.

 

D. SPATIAL

S'orienter à l'aide d'une carte.
Reconnaître des corps solides et des figures planes.

 

E. NUMERIQUE

Reconnaître les entiers naturels, utiliser la numération indo-arabe.
Reconnaître les quatre opérations arithmétiques.
Maîtriser les techniques opératoires de l'addition et de la soustraction.
S'entraîner aux techniques opératoires de la multiplication et de la division.
Appliquer des relations entre les nombres pour un calcul réfléchi.
Utiliser des fractions simples pour indiquer des parts.

 

F. MESURE

Effectuer des mesures de longueur, de masse et de durée.
Lire l'heure.

 
Premier Cycle: 1ère Année

SYLLABUS

ARITHMETIQUE ET ALGEBRE  (120 h)

1.  ENTIERS NATURELS (60 h)

  • Nombres inférieurs à 100.
  • Lecture, écriture en chiffres.
  • Comparaison.
  • Groupement par 10.

 

2.  ADDITION (50 h)

  • Addition des entiers.
  • Fonction "ajouter n".
  • Tables d'addition: construction (jusqu'à 9).
  • Technique opératoire avec retenue.
  • Décomposition d'un entier.

 

3.  SOUSTRACTION (10 h)

  • Initiation.

GEOMETRIE  (25 h)

1. LOCALISATION ET REPERAGE (10 h)

  • Domaine.
  • Déplacement.
  • Positionnement dans l'espace.

 

2. CORPS SOLIDES (5 h)

  • Pavé. Cube. Sphère. Cylindre. Cône.

 

3. FIGURES PLANES (5 h)

  • Lignes.
  • Carré. Rectangle. Triangle. Disque.

 

4. TRANSFORMATIONS (5 h)

  • Axe de symétrie.

 

MESURE (5 h)

1. LONGUEUR (5 h)

  • Comparaison de longueurs.

 

 

 
Premier Cycle: 2ème Année

                                                                                                                                                         SYLLABUS

 

ARITHMETIQUE ET ALGEBRE  (120 h)

1. ENTIERS NATURELS (25 h)

  • Nombres inférieurs à 1 000.
  • Lecture et écriture en lettres des nombres inférieurs à 100.
  • Ordre; signes < et >; représentation sur une droite.
  • Ecriture développée.

 

2. ADDITION (30 h)

  • Mémorisation des tables d'addition.
  • Maîtrise de la technique opératoire.

 

3. SOUSTRACTION (30 h)

  • Opération inverse de l'addition.
  • Fonction "soustraire n".
  • Technique opératoire: emprunt à l'unité contiguë.

 

4. MULTIPLICATION (30 h)

  • Addition itérative.
  • Table de multiplication: construction (jusqu'à 9).
  • Multiplication par un nombre à un chiffre.

 

5. DIVISION (5 h)

  • Initiation: partage, distribution.

 

 

GEOMETRIE  (25 h)

1. LOCALISATION ET REPERAGE (5 h)

  • Repérage d'un point.

 

2. CORPS SOLIDES (5 h)

  • Description de solides: sommets, arêtes et faces.

 

3. FIGURES PLANES (5 h)

  • Segment de droite.
  • Description de figures planes: sommets et côtés.

 

4. TRANSFORMATIONS (5 h)

  • Figures ayant un axe de symétrie.

 

MESURE  (5 h)

1. LONGUEUR (5 h)

  • Mesure de longueurs: le mètre, le centimètre.

 

2. MASSE (5 h)

  • Comparaison de masses.

 
 

 

EDUCATION DE BASE  - ENSEIGNEMENT PRIMAIRE 

Premier Cycle: 3ème Année

                                                                                                                                                         SYLLABUS

 

ARITHMETIQUE ET ALGEBRE  (110 h)

1. ENTIERS NATURELS (15 h)

  • Nombres inférieurs à 100 000.
  • Lecture et écriture en chiffres et en lettres.
  • Compatibilité de l'ordre avec l'addition, la soustraction et la multiplication.

 

2. FRACTIONS (5 h)

  • Fractions .

 

3. ADDITION (10 h)

  • Propriétés: la commutativité et l'associativité.

 

4. SOUSTRACTION (20 h)

  • Maîtrise de la technique opératoire.

 

5. MULTIPLICATION (30 h)

  • Fonction "multiplier par n".
  • Multiplication par 10 et par un multiple de 10.
  • Distributivité de la multiplication par rapport à l'addition.
  • Mémorisation des tables de multiplication.
  • Technique opératoire: multiplicateur à deux chiffres.

 

6. DIVISION (30 h)

  • Division exacte et division euclidienne.
  • Technique opératoire.

 

 

GEOMETRIE  (20 h)

1. LOCALISATION ET REPERAGE (5 h)

  • Milieu d'un segment de droite.
  • Droites perpendiculaires.

 

2. CORPS SOLIDES (7 h)

  • Construction d'un cube et d'un pavé.

 

3. FIGURES PLANES (3 h)

  • Angle droit. Application au rectangle et au carré.

 

4. TRANSFORMATIONS (5 h)

  • Réflexion.

 

MESURE  (20 h)

1. LONGUEUR (10 h)

  • Unités de longueur: kilomètre, mètre, centimètre, millimètre.
  • Distance entre deux points.
  • Longueur d'une ligne polygonale. Périmètre.

 

2. MASSE (5 h)

  • Kilogramme. Gramme.

 

3. TEMPS ET DUREE (5 h)

  • Lecture de l'heure.
  • Durée d'un événement.
  • Unités de temps: heure, minute, seconde.

 
 

 

 

ENSEIGNEMENT PRIMAIRE - SECOND CYCLE

 
OBJECTIFS

Le curriculum prévoit pour les élèves qui terminent ce cycle une formation nécessaire et durable, de sorte que ceux qui seront obligés de quitter l'école à 12 ans pour participer à la production, reçoivent et maîtrisent des aptitudes assurant leur non retour à l'analphabétisme mathématique. Ainsi les élèves doivent, dans les domaines suivants, être capables de:

 

A. RAISONNEMENT MATHEMATIQUE

Trouver des tendances dans des suites de résultats et les généraliser.
Dégager des énoncés généraux à partir de réalisations effectives.
Etablir des procédés.
Argumenter, par analogie et en donnant des exemples et des contre-exemples.

 

B. RESOLUTION DE PROBLEMES

Schématiser des situations et traiter des informations.
Utiliser et appliquer les Mathématiques dans différents domaines en particulier en technologie et dans les autres branches du savoir.
Vérifier les résultats.
Utiliser les calculettes pour effectuer les quatre opérations.

 

C. COMMUNICATION

Lire, comprendre et interpréter un texte mathématique en le traduisant en figures, représentations ou équations.
Traduire une relation mathématique donnée en langue parlée.

 

D. SPATIAL

Représenter des lieux sur une carte.
Caractériser différentes figures planes et utiliser les instruments de
Géométrie pour les représenter.
Réaliser le développement de quelques corps solides.

 

E. NUMERIQUE

Maîtriser le système de numération indo-arabe.
Reconnaître les nombres décimaux.   
Maîtriser tous les types de calcul différé, réfléchi et avec la calculette (entiers et décimaux).
Effectuer des opérations simples sur les fractions.
Estimer un résultat.

 

F. MESURE

Effectuer des mesures de périmètre, d'aire, de capacité et d'angle.
Utiliser les unités métriques.

 

G. STATISTIQUE

Collecter et interpréter des données.

 
Second Cycle: 4ème Année

SYLLABUS

 

ARITHMETIQUE ET ALGEBRE (110 h)

1. ENTIERS NATURELS (15 h)

  • Nombres supérieurs à 100 000.
  • Multiples d'un entier.
  • Critères de divisibilité par 2, 5 et 10.
  • Numération sexagésimale.

 

2. FRACTIONS (15 h)

  • Fractions  ( a £ b).
  • Comparaison de fractions.

 

3. DECIMAUX (10 h)

  • Nombres décimaux.

 

4. ADDITION (15 h)

  • Addition des décimaux.
  • Addition des fractions de même dénominateur.
  • Addition de durées et de temps.

 

5. SOUSTRACTION (15 h)

  • Soustraction de décimaux.
  • Soustraction de fractions de même dénominateur.
  • Soustraction de durées et de temps.

 

6. MULTIPLICATION (10 h)

  • Multiplication d'un décimal par un entier.
  • Propriétés: la commutativité et l'associativité.
  • Distributivité de la multiplication par rapport à l'addition et à la soustraction.

 

7. DIVISION (30 h)

  • Technique opératoire sur les entiers: diviseurs à deux chiffres au plus, quotient entier.
  • Fonction "diviser par n".

 

 

GEOMETRIE (20 h)

1. LOCALISATION ET REPERAGE (5 h)

  • Distance d'un point à une droite.
  • Localisation d'un point sur un quadrillage.

 

2. CORPS SOLIDES (5 h)

  • Construction de solides.

 

3. FIGURES PLANES (5 h)

  • Droites concourantes. Droites parallèles.
  • Classification des quadrilatères selon leurs côtés.
  • Cercle. Disque.

 

4. TRANSFORMATIONS (5 h)

  • Dessin du symétrique d'une figure par rapport à un axe.

 

MESURE (20 h)

1. LONGUEUR (6 h)

  • Système métrique des unités de longueur.

 

2. MASSE (3 h)

  • Système métrique des unités de masse.

 

3. SURFACE (3 h)

  • Comparaison d'aires.

 

4. CAPACITE (3 h)

  • Litre et sous-multiples.
  • Unités de temps: heure, minute, seconde.

 

STATISTIQUE (5 h)

1.GESTION DES DONNEES (5 h)

  • Collecte et organisation des données

 
 

 

 
Second Cycle: 5ème Année

SYLLABUS

 

ARITHMETIQUE ET ALGEBRE (100 h)

1. ENTIERS NATURELS (20 h)

  • Critères de divisibilité par 3, 4 et 9.
  • Multiples communs de deux entiers.
  • Diviseurs d'un entier.
  • Diviseurs communs de deux entiers.
  • Système de numération décimale.

 

2. FRACTIONS (10 h)

  • Egalité et simplification des fractions.
  • Nombres mixtes.

 

3. DECIMAUX (10 h)

  • Comparaison et représentation des nombres décimaux.

 

4. ADDITION (15 h)

  • Addition de fractions.
  • Addition de décimaux à plusieurs décimales.

 

5. SOUSTRACTION (15 h)

  • Soustraction de fractions.
  • Soustraction de décimaux à plusieurs décimales.

 

6. MULTIPLICATION (20 h)

  • Multiplication de décimaux.
  • Fonction "multiplier par ".
  • Produit d'une durée par un entier.

 

7. DIVISION (10 h)

  • Quotient décimal d'une division.

 

 

GEOMETRIE (25 h)

1. LOCALISATION ET REPERAGE (3 h)

  • Distance de deux droites parallèles.

 

2. CORPS SOLIDES (7 h)

  • Développement de solides.

 

3. FIGURES PLANES (10 h)

  • Angle.
  • Diagonales d'un polygone.
  • Classification des quadrilatères selon les diagonales.
  • Diamètre d'un cercle.

 

4. TRANSFORMATIONS (5 h)

  • Homothétie.

 

MESURE (20 h)

1. LONGUEUR (3 h)

  • Longueur d'un cercle.

 

2. SURFACE (10 h)

  • Aire du carré, rectangle, triangle rectangle, disque.

 

3. ANGLE (2 h)

  • Mesure d'un angle en degré.

 

4. CAPACITE (5 h)

  • Système métrique des unités de capacité.

 

STATISTIQUE (5 h)

1. GESTION DES DONNEES (5 h)

  • Représentation des données en bâtons, bandes et pictogramme.

 
 

 

 

 
Second Cycle: 6ème Année

SYLLABUS

 

ARITHMETIQUE ET ALGEBRE (110 h)

1. ENTIERS NATURELS (15 h)

  • Développement d'un entier naturel suivant les puissances de 10.
  • P.G.C.D et P.P.C.M de deux entiers naturels.
  • Nombres premiers entre eux.

 

2. FRACTIONS (10 h)

  • Fractions irréductibles.
  • Fractions décimales.

 

3. DECIMAUX (10 h)

  • Ecriture fractionnaire d'un nombre décimal.
  • Développement d'un nombre décimal selon les puissances de 10 et de .

 

4. NOMBRES RELATIFS (15 h)

  • Nombres positifs et nombres négatifs.
  • Représentation sur l'axe numérique.
  • Comparaison.

 

5. ADDITION (5 h)

  • Addition de nombres relatifs.

 

6. SOUSTRACTION (5 h)

  • Soustraction de nombres relatifs.

 

7. MULTIPLICATION (10 h)

  • Multiplication de fractions.
  • Puissances d'exposant 2 et 3.
  • Puissances de 10.

 

8. DIVISION (10 h)

  • Division des fractions.
  • Quotient et rapport.
  • Division d'une durée par un entier.

 

9. PROPORTIONNALITE (20 h)

  • Pourcentage. Taux.
  • Suites proportionnelles.
  • Echelle.

 

10. EXPRESSIONS ALGEBRIQUES (10 h)

  • Lois de priorités des opérations dans un calcul.
  • Calcul sur les expressions littérales.
  • Valeur numérique d'une expression littérale.

 

 

GEOMETRIE (25 h)

1. LOCALISATION ET REPERAGE (2 h)

  • Positions relatives de deux droites dans un plan.
  • Positions relatives d'une droite et d'un cercle.

 

2. CORPS SOLIDES (3 h)

  • Patrons de solides.

 

3. FIGURES PLANES (10 h)

  • Angles adjacents, angles opposés par le sommet.
  • Bissectrice d'un angle.
  • Médiatrice d'un segment de droite.
  • Triangle: triangles particuliers; droites particulières dans un triangle; somme des angles d'un triangle.

 

4. TRANSFORMATIONS (10 h)

  • Symétrie centrale.
  • Etude de figures à partir de leurs éléments de symétrie.

 

MESURE (20 h)

1. SURFACE (8 h)

  • Aire d'un parallélogramme, d'un triangle.
  • Système métrique des unités d'aire.

 

2. ANGLE (2 h)

  • Angles complémentaires; angles supplémentaires.

 

3. VOLUME (10 h)

  • Calcul de volume: cube, parallélépipède rectangle, cylindre droit, boule.
  • Système métrique des unités de volume.

 

STATISTIQUE (5 h)

1. GESTION DES DONNEES (5 h)

  •  Lecture d'un diagramme circulaire.

 
 

 

 

ENSEIGNEMENT PRIMAIRE – CYCLE MOYEN

 
OBJECTIFS

Le curriculum propose que, dans les domaines suivants, les élèves soient capables de:

 

A. RAISONNEMENT MATHEMATIQUE

Relier des observations du réel à des représentations et relier celles-ci à des concepts.
Induire le terme général d'une suite de résultats dûment construite.
Distinguer entre un énoncé général et un énoncé particulier.
Effectuer des démonstrations simples.  
Reconnaître une fausse démonstration.

 

B. RESOLUTION DE PROBLEMES

Analyser une situation pour en déduire les éléments pertinents.
Rechercher les informations nécessaires pour élucider une donnée incomplète.
Construire un modèle mathématique associé à une situation.
Choisir une stratégie pour trouver la solution.
Décomposer une difficulté en des tâches plus simples et réciproquement combiner des faits nécessaires pour conclure.
Utiliser les machines à calculer avec mémoire.

 

C. COMMUNICATION

Lire, comprendre et utiliser les notations et le langage mathématique.
Présenter leur travail avec clarté et rigueur oralement et par écrit, apporter
un soin particulier à la rédaction d'une démonstration.

 

D. SPATIAL

Construire des figures géométriques à partir de données.
Représenter des corps solides.
Démontrer et appliquer les propriétés des figures planes.
Effectuer des transformations affines sur les figures.

 

E. NUMERIQUE

Trouver et utiliser des relations entre les nombres.
Etendre les techniques opératoires à des expressions littérales.  
Trouver des valeurs approchées d'un résultat.

 

F. MESURE

Effectuer des mesures d'aires, de volumes.

 

G. STATISTIQUE

Faire et lire des représentations de données statistiques.
Calculer la moyenne d'une distribution statistique.

 
EDUCATION DE BASE - ENSEIGNEMENT PRIMAIRE - Cycle Moyen: 7ème Année

SYLLABUS

 

ARITHMETIQUE ET ALGEBRE (90 h)

1. ENTIERS NATURELS (10 h)

  • Nombres premiers.
  • Décomposition d'un entier en facteurs premiers.

 

2. FRACTIONS (10 h)

  • Réduction de fractions.

 

3. DECIMAUX (5 h)

  • Ecriture décimale d'une fraction.

 

4. OPERATIONS (30 h)

  • Soustraction et multiplication de nombres relatifs.
  • Puissances d'exposant entier positif d'un nombre positif.
  • Facteur commun. Factorisation.

 

5. PROPORTIONNALITE (10 h)

  • Grandeurs directement proportionnelles.

 

6. EXPRESSIONS ALGEBRIQUES (15 h)

  • Calcul sur des expressions algébriques.

 

7. EQUATIONS ET INEQUATIONS (10 h)

  • Equations se ramenant à ax = b.

 

 

GEOMETRIE (55 h)

1. LOCALISATION ET REPERAGE (10 h)

  • Lieux géométriques et constructions.
  • Repères orthogonaux et coordonnés d'un point dans un plan.

 

2. GEOMETIE DANS L'ESPACE (5 h)

  • Représentation plane d'un cube, d'un parallélépipède rectangle.

 

3. FIGURES PLANES (35 h)

  • Cas de superposition des triangles.
  • Angles formés par deux droites parallèles coupées par une sécante.
  • Propriétés caractéristiques de la médiatrice d'un segment de droite.
  • Propriétés caractéristiques de la bissectrice d'un angle.

 

4. TRANSFORMATIONS ET VECTEURS (5 h)

  • Translation.

 

STATISTIQUE (5 h)

1. GESTION DES DONNEES (5 h)

  • Fréquences relatives.
  • Représentations graphiques des données: diagramme en bâtons, polygone des fréquences.

 
 

 

 
EDUCATION DE BASE - ENSEIGNEMENT PRIMAIRE - Cycle Moyen: 8ème Année

SYLLABUS

 

ARITHMETIQUE ET ALGEBRE (70 h)

1. ENTIERS NATURELS (5 h)

  • P.G.C.D et P.P.C.M de plusieurs entiers.

 

2. FRACTIONS (5 h)

  • Fractions littérales.
  • Fractions composées.

 

3. DECIMAUX (5 h)

  • Compatibilité de l'ordre avec les opérations.

 

4. RACINES CARREES (10 h)

  • Racines carrées d'un nombre positif.

 

5. OPERATIONS (5 h)

  • Puissances d'exposant entier positif d'un nombre relatif.
  • Puissances d'exposant entier négatif de 10.

 

6. PROPORTIONNALITE (5 h)

  • Grandeurs inversement proportionnelles.

 

7. EXPRESSIONS ALGEBRIQUES (20 h)

  • Identités remarquables.
  • Expressions littérales sous forme fractionnaire.

 

8. EQUATIONS ET INEQUATIONS (15 h)

  • Equation du type (ax + b) (cx + d) = 0.
  • Equations et inéquations du premier degré à une inconnue.

 

 

GEOMETRIE (70 h)

1. LOCALISATION ET REPERAGE (15 h)

  • Positions relatives de deux cercles.
  • Lieux géométriques et constructions.
  • Coordonnées du milieu d'un segment de droite.

 

2. GEOMETRIE DANS L'ESPACE (10 h)

  • Représentation plane d'un cylindre, d'une pyramide, d'un cône, d'une sphère.
  • Positions relatives de droites et de plans.

 

3. FIGURES PLANES (40 h)

  • Théorème de Pythagore.
  • Théorème des milieux dans un triangle, dans un trapèze.
  • Propriétés caractéristiques du parallélogramme.
  • Angle au centre d'un cercle, angle inscrit dans un cercle. Aire d'un secteur circulaire.

 

4. TRANSFORMATIONS ET VECTEURS (5 h)

  • Vecteur et translation.

 

STATISTIQUE (10 h)

1. GESTION DES DONNEES (10 h)

  • Effectifs et fréquences cumulés.
  • Représentations graphiques des données: diagrammes circulaires, polygone des fréquences cumulées.

 
 

 

 

 
EDUCATION DE BASE - ENSEIGNEMENT PRIMAIRE - Cycle Moyen: 9ème Année

SYLLABUS

 

ARITHMETIQUE ET ALGEBRE (70 h)

1. NOMBRES REELS (5 h)

      Nombres rationnels et irrationnels.

 

2. OPERATIONS (10 h)

  • Rendre rationnel le dénominateur d'une fraction.
  • Calcul sur les réels.

 

3. PROPORTIONNALITE (5 h)

  • Fonctions linéaires et proportionnalité.

 

4. EXPRESSIONS ALGEBRIQUES (10 h)

  • Expressions algébriques comprenant de radicaux.  
  • Polynôme à une variable.

 

5. EQUATIONS ET INEQUATIONS (40 h)

  • Equations du type .
  • Systèmes d'équations du premier degré à deux inconnues.
  • Systèmes d'inéquations du premier degré à une inconnue.

.

 

 

GEOMETRIE (70 h)

1. LOCALISATION ET REPERAGE (35 h)

  • Tangentes et cercles.
  • Lieux géométriques et constructions.
  • Représentation graphique d'une droite.
  • Propriétés analytiques du parallélisme et de l'orthogonalité de deux droites.
  • Longueur d'un segment de droite dans un repère orthonormé.
  • Résolution graphique d'un système d'équations linéaires à deux inconnues.

 

2. GEOMETRIE DANS L'ESPACE (5 h)

  • Intersection d'une droite et d'un solide usuel.
  • Intersection d'un plan et d'un solide usuel.

 

3. FIGURES PLANES (20 h)

  • Quadrilatères inscriptibles.
  • Théorème de Thalès.   
  • Triangles semblables.

 

4. TRANSFORMATIONS ET VECTEURS (5 h)

  • Vecteur dans un plan.

 

5. TRIGONOMETRIE (5 h)

  • Sinus, cosinus et tangente d'un angle aigu dans un triangle rectangle.

 

STATISTIQUE (10 h)

1. GESTION DES DONNEES (10 h)

  • Série statistique à une variable discrète: différentes représentations.
  • Moyenne et moyenne pondérée.

 
 

 

 

ENSEIGNEMENT SECONDAIRE – SERIE LETTRES ET HUMANITES

 
OBJECTIFS

Le curriculum prévoit pour les Dans cette série les élèves apprennent à apprécier les Mathématiques comme activité intellectuelle fondamentale et utilisent leurs résultats pour traiter des informations recueillies en littérature et Sciences Humaines. Pour cela, dans les domaines suivants, ils doivent être capables de:

 

A. RAISONNEMENT MATHEMATIQUE

Reconnaître les différentes formes de raisonnement mathématique.

 

B. RESOLUTION DE PROBLEMES

Utiliser une interprétation mathématique adéquate pour représenter les données d'un problème.
Trouver la solution d'un problème en suivant un algorithme donné.

 

C. COMMUNICATION

Relever les formules et les relations d'un texte mathématique.
Rédiger leur travail avec précision.

 

D. SPATIAL

Représenter des corps solides.

 

E. NUMERIQUE ET ALGEBRIQUE

Analyser les causes d'extension des ensembles de nombres: NÌ Z Ì Q Ì R.
Généraliser des notions fondamentales déjà utilisées: ensemble, relation, loi de composition et calcul propositionnel.
Acquérir la notion de structure de groupe.
Résoudre des problèmes simples à une ou deux inconnues.

 

F. ANALYSE

Etudier et représenter des fonctions simples.
Relier la croissance exponentielle et la fonction exponentielle.
Calculer des intérêts simples ou composés.

 

G. STATISTIQUE ET PROBABILITE

Organiser des informations en les représentant graphiquement.
Etudier les caractéristiques d'une série statistique à une variable.
Résoudre des problèmes simples de probabilités surtout dans le cas discret où les éventualités sont équiprobables.

 
PROGRESSION DU CONTENU - Serie Letters et Humanités

 

  ALGEBRE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. FONDEMENTS

 
  • Ensembles.
  • Produit cartésien.
  • Application, bijection.
  • Relations binaires.

 

 
  • Loi de composition interne.
  • Structure de groupe.
  • Eléments de calcul de propositions.

 

(7 h)

(10 h)

(10 h)

2. CALCUL
NUMERIQUE ET
LITTERAL

 
  • Racines carrées d'un réel. Puissances d'un réel.
  • Ordre sur R. Intervalles.
  • Valeur absolue.
  • Encadrement. Approximation.
  • Dénombrement.
  • Arrangements et permutations.

 

 

(23 h)

(10 h)

 

3. EQUATIONS ET
INEQUATIONS
  • Equation du premier degré.
  • Equation et inéquation du premier degré faisant intervenir la valeur absolue.
  • Système d'équations linéaires (2 x 2).
  • 4. Résolution et interprétation géométrique d'un système d'inéquations linéaires à deux inconnues.                                     
  • Programmation linéaire.
  • Résolution d'une équation du second degré à coefficients réels.
  • Somme et produit des racines du trinôme du second degré.
  • Situations-problèmes se ramenant à la résolution d'équations et d'inéquations.

 

(15 h)

(15 h)

(10 h)

4. POLYNOMES
  • Polynômes.
  • Racine d'un polynôme.
  • Etude du signe du trinôme du second degré.

 

 

(8 h)

(5 h)

 

5. NOMBRES
  • Systèmes de nombres: N, Z, Q, R.

 

 

 

(2 h)

 

 
 

 

GEOMETRIE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. ETUDE CLASSIQUE
  • Représentation plane des objets de l'espace.
  • Intersection d'une droite ou d'un plan avec des solides usuels.
  • Droites et plans: positions relatives, parallélisme.

 

 

 

(17 h)

 

 

2. ETUDE VECTORIELLE
  • Vecteurs du plan.
  • Projection dans le plan.
  • Bases et repères du plan.                      

 

 

 

(20 h)

 

 

3. ETUDE ANALYTIQUE
  • Equations d'une droite dans le plan.
  • Produit scalaire.

 

 

 

(18 h)

 

 
 

 

ANALYSE (FONCTIONS NUMERIQUES)
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. DEFINITIONS ET

   REPRESENTATION
  • Fonctions. Représentation graphique.
  • Résolution graphique d'équations et d'inéquations.
  • Etude des fonctions usuelles.
  • Limite d'une fonction en un point. Limite à l'infini.
  • Asymptotes verticales et horizontales.
  • Calcul sur les limites.
  • Suites arithmétiques. Suites géométriques.               
  • Fonctions rationnelles simples.
  • Lecture graphique.
  • Croissance exponentielle et fonction exponentielle.

 

(20 h)

(15 h)

(15 h)

2. CONTINUITE ET

    DERIVATION

 
  • Continuité des fonctions usuelles.
  • Dérivée d'une fonction en un point.
  • Fonction dérivée. Dérivées des fonctions usuelles, règles de calcul.
  • Etude des fonctions: fonctions polynômes, fonctions  homographiques.

 

 

 

(25 h)

 

3. INTEGRATION

 
  • Primitives d'une fonction continue sur un intervalle: calcul de primitives.

 

 

 

(10 h)

 

4. MODELES
   MATHEMATIQUES
   POUR L'ECONOMIE ET

   LES SCIENCES SOCIALES

 

 
  • Intérêt simple, intérêt composé.

 

 

 

(10 h)
 

 

TRIGONOMETRIE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. LIGNES

   TRIGONOMETRIQUES
  • Cercle trigonométrique. Arc orienté.
  • Lignes trigonométriques d'un arc.

 

 

 

(10 h)

 

 
 

 

STATISTIQUE ET PROBABILITE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. STATISTIQUE

    
  • Vocabulaire statistique.
  • Représentation graphique d'une série statistique à une variable discrète.
  • Effectifs et fréquences cumulés.
  • Caractéristiques de position et de dispersion.
  • Variable continue; répartition en classes.
  • Séries statistiques des effectifs et des fréquences; histogramme, polygones.
  • Séries statistiques des effectifs et des fréquences cumulés; histogramme, polygones.
  • Caractéristiques de position et de dispersion d'une série statistique à une variable (continue ou discrète).

 

 

 

(10 h)

(15 h)

(10 h)

2. PROBABILITE

 
  • Notion de probabilité.
  • L'univers des possibles. Cas d'événements équiprobables.
  • Propriétés de la probabilité.
  • Calcul de probabilités: événement (A et B), événement (A ou B), événements incompatibles, événements contraires.
  • Probabilité conditionnelle: définition, indépendance de deux événements.

 

 

 

 

(15 h)

(5 h)
 

 

 

 

ENSEIGNEMENT SECONDAIRE – SERIE SOCIOLOGIE ET ECONOMIE

 
OBJECTIFS

Dans cette série les élèves apprennent à apprécier les Mathématiques comme outil indispensable au traitement des informations récueillies en Economie et dans les Sciences Sociales. Pour cela, et dans les domaines suivants, ils doivent être capables de:

 

A. RAISONNEMENT MATHEMATIQUE

Reconnaître la différence entre une explication mathématique et une évidence concrète ou expérimentale.
Faire des conjectures et imaginer un moyen de les tester.

 

B. RESOLUTION DE PROBLEMES

Formuler un problème à partir de situations étudiées en Economie et en Sciences Sociales.
Utiliser une interprétation mathématique adéquate pour représenter les données d'un problème.
Appliquer ses connaissances mathématiques pour trouver la solution d'un problème en suivant un algorithme convenable.
Discuter la validité des solutions obtenues.

 

C. COMMUNICATION

Comprendre un document mathématique consulté et en retenir les points essentiels.
Prendre des notes lors d'un exposé mathématique.

 

D. SPATIAL

Démontrer et appliquer les propriétés des corps solides.

 

E. NUMERIQUE ET ALGEBRIQUE

Analyser les causes d'extension des ensembles de nombres: NÌ Z Ì Q Ì R.
Généraliser des notions fondamentales déjà utilisées: ensemble, relation, loi de composition.
Acquérir la notion de structure de groupe.
Développer des outils mathématiques du calcul numérique, de la résolution de système d'équations et d'inéquations.

 

F. ANALYSE

Utiliser et interpréter graphiquement les notions de limite, de continuité, de dérivation pour étudier des fonctions numériques.
Analyser les graphiques des fonctions polynomiales, rationnelles, irrationnelles, trigonométriques, logarithmiques et exponentielles.
Intégrer une fonction et résoudre des équations différentielles simples.
Résoudre des équations aux différences finies.
Etudier des fonctions économiques et sociales.
Résoudre des problèmes de Mathématiques financières.

 

G. STATISTIQUE ET PROBABILITE

Organiser des informations en les représentant graphiquement.
Etudier les caractéristiques d'une série statistique à une ou deux variables.
Résoudre des problèmes simples de probabilités surtout dans le cas discret où les éventualités sont équiprobables.

 
PROGRESSION DU CONTENU - Serie Sociologie et Economie

  ALGEBRE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

 

1. FONDEMENTS

 

 
  • Ensembles.
  • Produit cartésien.
  • Application, bijection.
  • Relations binaires.

 

 
  • Loi de composition interne.
  • Structure de groupe.

 

 

(7 h)

(10 h)

(8 h)

 

2. CALCUL
NUMERIQUE ET
LITTERAL

 
  • Racines carrées d'un réel. Puissances d'un réel.
  • Ordre sur R. Intervalles.
  • Valeur absolue.
  • Encadrement. Approximation.
  • Dénombrement.
  • Arrangements et permutations.

 

 

 

 

 
  • Combinaisons: définition, notation, formule du binôme.

 

 

 

 

 

(23 h)

(10 h)

(7 h)

 

3. EQUATIONS ET INEQUATIONS
  • Equation du premier degré.
  • Equation et inéquation du premier degré faisant intervenir la valeur absolue.
  • Système d'équations linéaires (2 x 2).
  • Résolution et interprétation géométrique d'un système d'inéquations linéaires à deux inconnues.
  • Programmation linéaire.
  • Résolution d'une équation du second degré à coefficients réels.
  • Somme et produit des racines du trinôme du second degré.

 

 
  • Système d'équations linéaires (m x n): définition, opérations élémentaires sur les lignes, méthode de Gauss.

 

 

 

 

 

(15 h)

(15 h)

(10 h)

 

4. POLYNOMES
  • Polynômes.
  • Racine d'un polynôme.
  • Etude du signe du trinôme du second degré.

 

 

(8 h)

(5 h)

 

 

5. NOMBRES
  • Systèmes de nombres: N, Z, Q, R.

 

 

 

(2 h)

 

 
 

 

GEOMETRIE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

 

1. ETUDE CLASSIQUE
  • Représentation plane des objets de l'espace.
  • Intersection d'une droite ou d'un plan avec des solides usuels.
  • Droites et plans: positions relatives, parallélisme.     

 

 

 

(17 h)

 

 

 

2. ETUDE VECTORIELLE
  • Vecteurs du plan.
  • Projection dans le plan.
  • Bases et repères du plan.       

 

 

 

(20 h)

 

 

 

3. ETUDE ANALYTIQUE
  • Equations d'une droite dans le plan.
  • Produit scalaire.

 

 

 

(18 h)

 

 
 

 

ANALYSE (FONCTIONS NUMERIQUES)
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. DEFINITIONS ET       

   REPRESENTATION
  • Fonctions. Représentation graphique.
  • Résolution graphique d'équations et d'inéquations.
  • Etude des fonctions usuelles.

 

 

 
  • Limite d'une fonction en un point. Limite à l'infini. Asymptotes verticales et horizontales.
  • Calcul sur les limites.
  • Suites arithmétiques. Suites géométriques.

 

 
  • Fonctions rationnelles.
  • Fonction réciproque.
  • Fonction logarithme népérien. Fonction logarithme à base a.
  • Fonctions exponentielles.
  • Suites numériques. Suites géométriques: limites.

 

(20 h)

(15 h)

(20 h)

2. CONTINUITE ET

DERIVATION

 
  • Continuité des fonctions usuelles.
  • Dérivée d'une fonction en un point.
  • Fonction dérivée. Dérivées des fonctions usuelles, règles de calcul.
  • Etude des fonctions: fonctions polynômes, fonctions homographiques.

 
  • Dérivation des fonctions composées.
  • Dérivée seconde.
  • Règle de l'Hôpital.

 

 

 

 

 

 

(25 h)

(5 h)

3. INTEGRATION

 
  • Primitives d'une fonction continue sur un intervalle: calcul de primitives.

 
  • Intégrale: définition, propriétés, calcul.

 

 

 

 

(10 h)

(10 h)

4. EQUATIONS

    DIFFERENTIELLES

 

 
  • Définition.
  • Equations à variables séparables.
  • Equations linéaires du premier ordre à coefficients constants.
  • Equations aux différences finies.

 

 

 

 

(10 h)

5. MODELES

MATHEMATIQUES POUR L'ECONOMIE ET LES SCIENCES SOCIALES

 

 
  • Fonctions de l'économie et des sciences sociales.
  • Mathématiques financières.

 

 

 

(15 h)
 

 

TRIGONOMETRIE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. LIGNES TRIGONOMETRIQUES
  • Cercle trigonométrique. Arc orienté.
  • Lignes trigonométriques d'un arc. 

 

 

 

(10 h)

 

 
 

 

STATISTIQUE  ET  PROBABILITE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. STATISTIQUE

 
  • Vocabulaire statistique.
  • Représentation graphique d'une série statistique à une variable discrète.
  • Effectifs et fréquences cumulés.
  • Caractéristiques de position et de dispersion.

 

 
  • Variable continue; répartition en classes.
  • Séries statistiques des effectifs et des fréquences; histogramme, polygones.
  • Séries statistiques des effectifs et des fréquences cumulés; histogramme, polygones.

 

 
  • Caractéristiques de position et de dispersion d'une série statistique à une variable (continue ou discrète).
  • Série statistique à deux variables: introduction, nuage de points, point moyen.
  • Covariance de deux variables, coefficient de corrélation linéaire.
  • Ajustement linéaire et droit de regression.

 

(10 h)

(15 h)

(15 h)

2. PROBABILITE

 
  • Notion de probabilité.
  • L'univers des possibles. Cas d'événements équiprobables.
  • Propriétés de la probabilité.
  • Calcul de probabilités: événement (A et B), événement (A ou B), événements incompatibles, événements contraires.
  • Probabilité conditionnelle: définition, indépendance de deux événements.
  • Formule des probabilités totales.
  • Variable aléatoire réelle, loi de probabilité associée, fonction de répartition. Caractéristiques.

 

 

 

(15 h)

  (20 h)
 

 

 

 

ENSEIGNEMENT SECONDAIRE – SERIE SCIENCES GENERALES

 
OBJECTIFS

Cette série dote les élèves d'une formation mathématique de qualité en vue de les préparer à poursuivre leurs études supérieures d'enseignants, d'ingénieurs, et de chercheurs. C'est pourquoi, dans les domaines suivants, les élèves doivent être capables de:

 

A. RAISONNEMENT MATHEMATIQUE    

Reconnaître la différence entre une explication mathématique et une évidence concrète ou expérimentale.   
Faire des conjectures et imaginer un moyen de les tester.   
Effectuer des démonstrations en utilisant différents modes de raisonnement.   
Analyser et démontrer un énoncé de condition nécessaire et suffisante.   
Reconnaître un énoncé universel, d'existence, d'unicité.   
Evaluer un argument mathématique et critiquer une démonstration.   
Effectuer un raisonnemnt par récurrence.

 

B. RESOLUTION DE PROBLEMES   

Formuler un problème à partir de situations étudiées en Mathématiques, dans les autres sciences ou rencontrées dans la vie courante.   
Utiliser différentes interprétations mathématiques pour représenter les données d'un problème, imaginer une stratégie convenable à sa résolution et effectuer différentes approches pour réaliser cette stratégie en utilisant ses connaissances mathématiques.   
Discuter la validité des solutions obtenues.

 

C. COMMUNICATION   

Faire un exposé sur un document mathématique consulté.   
Prendre des notes lors d'un exposé mathématique.   
Effectuer une critique d'une présentation mathématique.   
Rédiger correctement une démonstration.

D. SPATIAL   

Démontrer et appliquer les propriétés des corps solides, des coniques.   
Caractériser les figures planes ou spatiales en utilisant les notions vectorielles.   
Etudier analytiquement des problèmes de Géométrie.   
Déterminer les effets des transformations sur les figures planes.

 

E. NUMERIQUE ET ALGEBRIQUE   

Analyser les causes d'extension des ensembles de nombres: NÌ Z Ì Q Ì R Ì C.   
Etudier les propriétés des nombres complexes et leur utilisation en Géométrie et en Trigonométrie.   
Généraliser des notions fondamentales déjà utilisées: ensemble, relation, loi de  composition et calcul propositionnel.   
Acquérir un exemple de structure.   
Développer des outils mathématiques de calcul numérique, de résolution de système d'équations et d'inéquations.    

 

F. ANALYSE   

Acquérir les concepts fondamentaux de limite, de continuité, de dérivation et les utiliser pour représenter graphiquement les variations d'une fonction numérique quelconque.   
Analyser les graphiques des fonctions polynomiales, rationnelles, irrationnelles, trigonométriques, logarithmiques et exponentielles.   
Intégrer une fonction et résoudre des équations différentielles simples.   

 

G. STATISTIQUE ET PROBABILITE   

Organiser des informations en les représentant graphiquement.   
Etudier les caractéristiques d'une série statistique à une variable.   
Résoudre des problèmes simples de probabilités surtout dans le cas discret où les éventualités sont équiprobables.

 
ENSEIGNEMENT SECONDAIRE - PROGRESSION DU CONTENU - Série Sciences Générales

  ALGEBRE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

 1. FONDEMENTS

 
  • Ensembles.
  • Produit cartésien.
  • Application, bijection.
  • Relations binaires.

 

 
  • Loi de composition interne.
  • Structure de groupe.
  • Eléments de calcul de propositions.

 

(7 h)

(6 h)

(15 h)

2. CALCUL MUMERIQUE  ET LITTERAL

 
  • Racines carrées d'un réel. Puissances d'un réel.
  • Ordre sur R. Intervalles.
  • Valeur absolue.
  • Encadrement. Approximation.
  • Dénombrement.
  • Arrangements et permutations.

 

 

 

 

 
  • Combinaisons: définition, notation, formule du binôme, triangle de Pascal.

 

 

 

 

 

(23 h)

(6 h)

(10 h)

3. EQUATIONS ET
INEQUATIONS

  • Equation du premier degré.
  • Equation et inéquation du premier degré faisant intervenir la valeur absolue.
  • Système d'équations linéaires (2 x 2).
  • Résolution et interprétation géométrique d'un système d'inéquations linéaires à deux inconnues.
  • Système d'équations linéaires (3x3). Programmation linéaire.
  • Polynômes, équations et inéquations du second degré.

 

 

 
  • Système d'équations linéaires (m x n): définition, opérations élémentaires sur les lignes, méthode de Gauss.
  • Equation du second degré à coefficients complexes.

 

 

 

(15 h)

(20 h)

(10 h)

4. POLYNOMES
  • Polynômes.
  • Racine d'un polynôme.

 

 
  • Division euclidienne d'un polynôme par un autre.
  • Factorisation. Simplification de fractions rationnelles.

 

 

(8 h)

(4 h)

 

5.NOMBRES

 
  • Systèmes de nombres: N, Z, Q, R.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 
  • Nombres complexes: définition, forme algébrique.
  • Opérations sur les nombres complexes.
  • Représentation géométrique d'un nombre complexe.

 

 

 

 

 

 

 

 

 

 

 

 
  • Module et argument d'un nombre complexe. Propriétés.
  • Forme trigonométrique et exponentielle d'un nombre complexe.
  • Interprétation géométrique de l'addition, de la multiplication des nombres complexes et du passage au conjugué.
  • Formule de Moivre. Applications.
  • Racines nème d'un nombre complexe, représentation géométrique des racines nème de l'unité.
  • Interprétation géométrique de  et de
  •  Applications.  

 

(2 h)

(8 h)

(25 h)
 

 

GEOMETRIE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

 

1. ETUDE CLASSIQUE
  • Représentation plane des objets de l'espace.
  • Intersection d'une droite ou d'un plan avec des solides usuels.
  • Droites et plans: positions relatives, parallélisme.
  • Orthogonalité dans l'espace.
  • Projections dans l'espace.
  • Les solides.

 

 

 
  • Coniques: définition, foyers, directrice, excentricité,  axe focal.
  • Equation d'une conique, sommets, centre, éléments de symétrie, équation réduite.
  • Courbes du second degré.         

 

 

(17 h)

(18 h)

(20 h)

2. ETUDE VECTORIELLE
  • Vecteurs du plan.
  • Projection dans le plan.
  • Bases et repères du plan.
  • Vecteurs et repères dans l'espace.
  • Barycentre.
  • Produit vectoriel.

 
  • Lignes de niveau
  • Equation vectorielle d'une droite, d'un plan, d'une sphère.

 

(20 h)

(16 h)

(5 h)

3. ETUDE ANALYTIQUE
  • Equations d'une droite dans le plan.
  • Produit scalaire.
  • Equation d'un cercle.
  • Produit scalaire dans l'espace.
  • Composantes du produit vectoriel. Produit mixte.
  • Equation d'un plan et d'une droite dans l'espace.
  • Orthogonalité de deux droites, d'une droite et d'un plan; plans perpendiculaires.
  • Parallélisme des droites et des plans.
  • Distance d'un point à un plan, à une droite.
  • Equation d'une sphère.
  • Intersection d'une sphère avec une droite, un plan ou une sphère.                                     

 

(18 h)

(9 h)

(30 h)

4. TRANSFORMATIONS PLANES

 
  • Isométrie. Translation.
  • Rotation plane.
  • Réflexion.
  • Déplacements dans le plan.
  • Homothétie.
  • Forme complexe d'une transformation plane.
  • Similitudes planes directes: définition, forme complexe.
  • Transformations définies par:
     et

 

 

(16 h)

(35 h)
 

 

ANALYSE (FONCTIONS NUMERIQUES)
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

 

1.  DEFINITIONS ET

 REPRESENTATION
  • Fonctions. Représentation graphique.
  • Résolution graphique d'équations et d'inéquations.
  • Etude des fonctions usuelles.
  • Limite d'une fonction. Asymptotes.
  • Suites numériques. Suites arithmétiques. Suites géométriques.
  • Fonctions irrationnelles (cas simples).
  • Fonction réciproque.
  • Fonctions trigonométriques inverses.
  • Fonction logarithme népérien. Fonction logarithme à base a.
  • Fonctions exponentielles. Fonctions puissances.
  • Suites numériques: limites, suites bornées, suites   convergentes.
  • Courbes paramétrées.

 

(20 h)

(14 h)

(40 h)

 

2. CONTINUITE ET

    DERIVATION

 
  • Continuité.
  • Dérivée d'une fonction en un point.
  • Fonction dérivée.
  • Etude des fonctions: fonctions polynômes, fonctions  rationnelles.
  • Image d'un intervalle fermé par une fonction continue. 
  • Prolongement par continuité d'une fonction.
  • Dérivation des fonctions composées.
  • Dérivée d'une fonction réciproque.
  • Dérivée seconde. Dérivées successives.
  • Théorème de Rolle. Egalité et inégalités des accroissements finis. Règle de l'Hôpital.

 

 

(22 h)

(25 h)

3. INTEGRATION

 
  • Primitives d'une fonction continue sur un intervalle.
  • Intégrale: définition, propriétés
  • Méthodes d'intégration.
  • Théorème de la moyenne.  Inégalités de la moyenne.
  • Applications du calcul intégral.

 

 

(6 h)

(30 h)

4. EQUATIONS

    DIFFERENTIELLES

 

 
  • Définition.
  • Equations à variables séparables.
  • Equations linéaires du premier ordre à coefficients constants.
  • Equations linéaires du second ordre à coefficients constants.

 

 

 

(10 h)
 

 

TRIGONOMETRIE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. LIGNES

TRIGONOMETRIQUES
  • Cercle trigonométrique. Arc orienté.
  • Lignes trigonométriques d'un arc.
  • Angle orienté de deux vecteurs.
  • Formules trigonométriques usuelles.
  • Relations métriques dans un triangle. Calcul d'aires.

 

(10 h)

(4 h)

(5 h)

2. EQUATIONS
TRIGONOMETRIQUES

 
  • Résolutions des équations de la forme:

    sinx = a, cosx = a, tanx = a.
  • Résolution d'équations trigonométriques simples.

 

 

(7 h)

  (5 h)

3. FONCTIONS
CIRCULAIRES

 
  • Etude des fonctions circulaires.
  • Etude des fonctions circulaires de la forme: 

    a cos (bx + c) et a sin (bx + c).

 

 

(4 h)

(5 h)
 

 

STATISTIQUE ET PROBABILITE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. STATISTIQUE

 
  • Vocabulaire statistique.
  • Représentation graphique d'une série statistique à une variable discrète.
  • Effectifs et fréquences cumulés.
  • Caractéristiques de position et de dispersion.
  • Variable continue; répartition en classes.
  • Séries statistiques des effectifs et des fréquences; histogramme, polygones.
  • Séries statistiques des effectifs et des fréquences cumulés; histogramme, polygones.
  • Caractéristiques de position et de dispersion d'une série statistique à une variable (continue ou discrète).

 

(10 h)

(8 h)

(10 h)

2. PROBABILITE

 
  • Notion de probabilité.
  • L'univers des possibles. Cas d'événements équiprobables.
  • Propriétés de la probabilité.
  • Calcul de probabilités: événement (A et B), événement (A ou B), événements incompatibles, événements contraires.
  • Probabilité conditionnelle: définition, indépendance de deux  événements.
  • Formule des probabilités totales.
  • Variable aléatoire réelle, loi de probabilité associée, fonction de répartition. Caractéristiques.

 

 

(12 h)

(20 h)
 

 

 

ENSEIGNEMENT SECONDAIRE – SERIE SCIENCES DE LA VIE

 
OBJECTIFS

Dans cette série les élèves reçoivent une solide formation mathématique et des connaissances nécessaires pour comprendre et traiter les problèmes rencontrés dans les sciences expérimentales et dans la vie courante. C'est pourquoi, dans les domaines suivants, ils doivent être capables de:

 

A. RAISONNEMENT MATHEMATIQUE    

Reconnaître la différence entre une explication mathématique et une évidence concrète ou expérimentale.   
Faire des conjectures et imaginer un moyen de les tester.   
Effectuer des démonstrations en utilisant différents modes de raisonnement.   
Analyser et démontrer un énoncé de condition nécessaire et suffisante.   
Reconnaître un énoncé universel, d'existence, d'unicité.   

 

B. RESOLUTION DE PROBLEMES

Formuler un problème à partir de situations étudiées dans les autres sciences.
Utiliser des moyens mathématiques adéquats pour représenter les données d'un problème.
Appliquer ses connaissances mathématiques pour trouver la solution d'un problème en suivant une stratégie convenable.

 

C. COMMUNICATION

Comprendre un document mathématique consulté et en retenir les points essentiels.
Prendre des notes lors d'un exposé mathématique.
Rédiger correctement une démonstration.

 

D. SPATIAL

Démontrer et appliquer les propriétés des corps solides.
Utiliser les notions vectorielles comme outil d'étude dans différentes disciplines.
Etudier analytiquement un problème de Géométrie.

 

E. NUMERIQUE ET ALGEBRIQUE   

Analyser les causes d'extension des ensembles de nombres: NÌ Z Ì Q Ì R Ì C.   
Etudier les propriétés des nombres complexes.
Généraliser des notions fondamentales déjà utilisées: ensemble, relation, loi de composition.
Acquérir la notion de structure de groupe.
Développer des outils mathématiques de calcul numérique, de résolution de système d'équations et d'inéquations.

 

F. ANALYSE

Acquérir les concepts fondamentaux de limite, de continuité, de dérivation et les utiliser pour étudier graphiquement des             relations fonctionnelles provenant des autres sciences.
Analyser les graphiques des fonctions polynomiales, rationnelles, irrationnelles, trigonométriques, logarithmiques et exponentielles.
Intégrer une fonction et résoudre des équations différentielles simples.

 

G. STATISTIQUE ET PROBABILITE

Organiser des informations en les représentant graphiquement.
Etudier les caractéristiques d'une série statistique à une variable.
Résoudre des problèmes simples de probabilités surtout dans le cas discret où les éventualités sont équiprobables.
Construire une loi de probabilité dans un cas simple et expliquer ses caractéristiques.

 
PROGRESSION DU CONTENU - Série Sciences de la Vie

  ALGEBRE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

 1. FONDEMENTS

 
  • Ensembles.
  • Produit cartésien.
  • Application, bijection.
  • Relations binaires.

 

 
  • Loi de composition interne.
  • Structure de groupe.

 

 

(7 h)

(6 h)

(8 h)

2. CALCUL MUMERIQUE  ET LITTERAL

 
  • Racines carrées d'un réel. Puissances d'un réel.
  • Ordre sur R. Intervalles.
  • Valeur absolue.
  • Encadrement. Approximation.
  • Dénombrement.
  • Arrangements et permutations.

 

 

 

 

 
  • Combinaisons: définition, notation, formule du binôme, triangle de Pascal.

 

 

 

 

 

(23 h)

(6 h)

(10 h)

3. EQUATIONS ET
INEQUATIONS

  • Equation du premier degré.
  • Equation et inéquation du premier degré faisant intervenir la valeur absolue.
  • Système d'équations linéaires (2 x 2).
  • Résolution et interprétation géométrique d'un système d'inéquations linéaires à deux inconnues.
  • Système d'équations linéaires (3x3). Programmation linéaire.
  • Polynômes, équations et inéquations du second degré.

 

 

 
  • Système d'équations linéaires (m x n): définition, opérations élémentaires sur les lignes, méthode de Gauss.

 

 

 

(15 h)

(20 h)

(7 h)

4. POLYNOMES
  • Polynômes.
  • Racine d'un polynôme.

 

 
  • Division euclidienne d'un polynôme par un autre.
  • Factorisation. Simplification de fractions rationnelles.

 

 

(8 h)

(4 h)

 

5.NOMBRES
  • Systèmes de nombres: N, Z, Q, R.
  • Nombres complexes: définition, forme algébrique.
  • Opérations sur les nombres complexes.
  • Représentation géométrique d'un nombre complexe.
  • Module et argument d'un nombre complexe. Propriétés.
  • Forme trigonométrique et exponentielle d'un nombre complexe.
  • Interprétation géométrique de l'addition, de la multiplication des nombres complexes et du passage au conjugué.
  • Formule de Moivre. Applications.

 

(2 h)

(8 h)

(10 h)
 

 

GEOMETRIE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

 

1. ETUDE CLASSIQUE
  • Représentation plane des objets de l'espace.
  • Intersection d'une droite ou d'un plan avec des solides usuels.
  • Droites et plans: positions relatives, parallélisme.
  • Orthogonalité dans l'espace.
  • Projections dans l'espace.
  • Les solides.

 

 

 

 

 

 

(17 h)

(18 h)

 

2. ETUDE VECTORIELLE
  • Vecteurs du plan.
  • Projection dans le plan.
  • Bases et repères du plan.
  • Vecteurs et repères dans l'espace.
  • Barycentre.
  • Produit vectoriel.

 

 

(20 h)

(16 h)

 

3. ETUDE ANALYTIQUE
  • Equations d'une droite dans le plan.
  • Produit scalaire.
  • Equation d'un cercle.
  • Produit scalaire dans l'espace.
  • Composantes du produit vectoriel. Produit mixte.
  • Equation d'un plan et d'une droite dans l'espace.
  • Orthogonalité de deux droites, d'une droite et d'un plan; plans perpendiculaires.
  • Parallélisme des droites et des plans.
  • Distance d'un point à un plan, à une droite.

                                

 

(18 h)

(9 h)

(15 h)

4. TRANSFORMATIONS PLANES

 
  • Isométrie. Translation.
  • Rotation plane.
  • Réflexion.

 

 

 

(16 h)

 
 

 

ANALYSE (FONCTIONS NUMERIQUES)
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

 

1.  DEFINITIONS ET

 REPRESENTATION
  • Fonctions. Représentation graphique.
  • Résolution graphique d'équations et d'inéquations.
  • Etude des fonctions usuelles.
  • Limite d'une fonction. Asymptotes.
  • Suites numériques. Suites arithmétiques. Suites géométriques.
  • Fonctions irrationnelles (cas simples).
  • Fonction réciproque.
  • Fonctions trigonométriques inverses.
  • Fonction logarithme népérien. Fonction logarithme à base a.
  • Fonctions exponentielles.

 

(20 h)

(14 h)

(25 h)

 

2. CONTINUITE ET

    DERIVATION

 
  • Continuité.
  • Dérivée d'une fonction en un point.
  • Fonction dérivée.
  • Etude des fonctions: fonctions polynômes, fonctions rationnelles.
  • Image d'un intervalle fermé par une fonction continue. 
  • Dérivation des fonctions composées.
  • Dérivée d'une fonction réciproque.
  • Dérivée seconde. Dérivées successives.
  • Règle de l'Hôpital.

 

 

(22 h)

(15 h)

3. INTEGRATION

 
  • Primitives d'une fonction continue sur un intervalle.
  • Intégrale: définition, propriétés.
  • Méthodes d'intégration.
  • Applications du calcul intégral.

 

 

(6 h)

(15 h)

4. EQUATIONS

    DIFFERENTIELLES

 

 
  • Définition.
  • Equations à variables séparables.
  • Equations linéaires du premier ordre à coefficients constants.
  • Equations linéaires du second ordre à coefficients constants.

 

 

 

(10 h)
 

 

TRIGONOMETRIE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. LIGNES

TRIGONOMETRIQUES
  • Cercle trigonométrique. Arc orienté.
  • Lignes trigonométriques d'un arc.
  • Angle orienté de deux vecteurs.
  • Formules trigonométriques usuelles.

 

 

(10 h)

(4 h)

 

2. EQUATIONS
TRIGONOMETRIQUES

 
  • Résolutions des équations de la forme:

    sinx = a, cosx = a, tanx = a.

 

 

 

(7 h)

 

3. FONCTIONS
CIRCULAIRES

 
  • Etude des fonctions circulaires.
  • Etude des fonctions circulaires de la forme: a cos (bx + c) et a sin (bx + c).

 

 

(4 h)

(5 h)
 

 

STATISTIQUE ET PROBABILITE
 

 

Classe

1ère année

2ème année

3ème année

Sujet

 

 

 

1. STATISTIQUE

 
  • Vocabulaire statistique.
  • Représentation graphique d'une série statistique à une variable discrète.
  • Effectifs et fréquences cumulés.
  • Caractéristiques de position et de dispersion.
  • Variable continue; répartition en classes.
  • Séries statistiques des effectifs et des fréquences; histogramme, polygones.
  • Séries statistiques des effectifs et des fréquences cumulés; histogramme, polygones.
  • Caractéristiques de position et de dispersion d'une série statistique à une variable (continue ou discrète).

 

(10 h)

(8 h)

(10 h)

2. PROBABILITE

 
  • Notion de probabilité.
  • L'univers des possibles. Cas d'événements équiprobables.
  • Propriétés de la probabilité.
  • Calcul de probabilités: événement (A et B), événement (A ou B), événements incompatibles, événements contraires.
  • Probabilité conditionnelle: définition, indépendance de deux  événements.
  • Formule des probabilités totales.
  • Variable aléatoire réelle, loi de probabilité associée, fonction de répartition. Caractéristiques.
  • Variable de Bernoulli.
  • Loi binomiale.

 

 

(12 h)

(20 h)
 

 

SYLLABUS

 
1ère Année Secondaire

 SYLLABUS

 

ALGEBRE (55 h)

1. FONDEMENTS (7 h)

  • Ensembles.
  • Produit cartésien.
  • Application, bijection.

 

2. CALCUL NUMERIQUE ET LITTERAL (23 h)

  • Racines carrées d'un réel. Puissances d'un réel.
  • Ordre sur R. Intervalles.
  • Valeur absolue.
  • Encadrement. Approximation.
  • Dénombrement.

 

3. EQUATIONS ET INEQUATIONS (15 h)

  • Equation du premier degré.
  • Equation et inéquation du premier degré faisant intervenir la valeur absolue.
  • Système d'équations linéaires (2 x 2).
  • Résolution et interprétation géométrique d'un système d'inéquations linéaires à deux inconnues.

 

4. POLYNOMES (8 h)

  • Polynômes.
  • Racine d'un polynôme.

 

5. NOMBRES (2 h)

  • Systèmes de nombres: N, Z, Q, R .

 

 

GEOMETRIE (55 h)

1. ETUDE CLASSIQUE (17 h)

  • Représentation plane des objets de l'espace.
  • Intersection d'une droite ou d'un plan avec des solides usuels.
  • Droites et plans: positions relatives, parallélisme.

 

2. ETUDE VECTORIELLE (20 h)

  • Vecteurs du plan.
  • Projection dans le plan.
  • Bases et repères du plan.

 

3. ETUDE ANALYTIQUE (18 h)

  • Equations d'une droite dans le plan.
  • Produit scalaire.

 

 

ANALYSE (FONCTIONS NUMERIQUES) (20 h)

1. DEFINITIONS ET REPRESENTATION (20 h)

  • Fonctions. Représentation graphique.
  • Résolution graphique d'équations et d'inéquations.
  • Etude des fonctions usuelles.

 

 

TRIGONOMETRIE (10 h)

1. LIGNES TRIGONOMETRIQUES (10 h)

  • Cercle trigonométrique. Arc orienté.
  • Lignes trigonométriques d'un arc.

 

STATISTIQUE (10 h)

1. STATISTIQUE (10 h)

  • Vocabulaire statistique.
  • Représentation graphique d'une série statistique à une variable discrète.
  • Effectifs et fréquences cumulés.
  • Caractéristiques de position et de dispersion.

 
 

 

 
2ème Année Secondaire – Série Humanités

SYLLABUS

 

ALGEBRE (40 h)

1. FONDEMENTS (10 h)

  • Relations binaires.

 

2. CALCUL NUMERIQUE ET LITTERAL (10 h)

  • Arrangements et permutations.

 

3. EQUATIONS ET INEQUATIONS (15 h)

  • Programmation linéaire.
  • Résolution d'une équation du second degré à coefficients réels.
  • Somme et produit des racines du trinôme du second degré.

 

4. POLYNOMES (5 h)

  •  Etude du signe du trinôme du second degré.

 

 

ANALYSE (FONCTIONS NUMERIQUES) (50 h)

1. DEFINITIONS ET REPRESENTATION (15 h)

  • Limite d'une fonction en un point. Limite à l'infini. Asymptotes verticales et horizontales.
  • Calcul sur les limites.
  • Suites arithmétiques. Suites géométriques.

 

2. CONTINUITE ET DERIVATION (25 h)

  • Continuité des fonctions usuelles.
  • Dérivée d'une fonction en un point.
  • Fonction dérivée. Dérivées des fonctions usuelles, règles de calcul.
  • Etude des fonctions: fonctions polynômes, fonctions homographiques.

 

3. INTEGRATION (10 h)

  • Primitives d'une fonction continue sur un intervalle: calcul de primitives.

 

STATISTIQUE (30h)

1. STATISTIQUE (15 h)

  • Variable continue; répartition en classes.
  • Séries statistiques des effectifs et des fréquences; histogramme, polygones.
  • Séries statistiques des effectifs et des fréquences cumulés; histogramme, polygones.

 

2. PROBABILITE (15 h)

  • Notion de probabilité.
  • L'univers des possibles. Cas d'événements équiprobables.
  • Propriétés de la probabilité.
  • Calcul de probabilités: événement (A et B), événement (A ou B), événements incompatibles, événements contraires.

 
 

 

 
2ème Année Secondaire – Série Scientifiques

SYLLABUS

 

ALGEBRE (44 h)

1. FONDEMENTS (6 h)

  • Relations binaires.

 

2. CALCUL NUMERIQUE ET LITTERAL (6 h)

  • Arrangements et permutations.

 

3. EQUATIONS ET INEQUATIONS (20 h)

  • Système d'équations linéaires (3x3). Programmation linéaire.
  • Polynômes, équations et inéquations du second degré.

 

4. POLYNOMES (4 h)

  • Division euclidienne d'un polynôme par un autre.
  • Factorisation. Simplification de fractions rationnelles.

 

5. NOMBRES (8 h)

  • Nombres complexes: définition, forme algébrique.
  • Opérations sur les nombres complexes.
  • Représentation géométrique d'un nombre complexe.

 

 

GEOMETRIE (59 h)

1. ETUDE CLASSIQUE (18 h)

  • Orthogonalité dans l'espace.
  • Projections dans l'espace.
  • Les solides.

 

2. ETUDE VECTORIELLE (16 h)

  • Vecteurs et repères dans l'espace.
  • Barycentre.
  • Produit vectoriel.

 

3. ETUDE ANALYTIQUE (9 h)

  • Equation d'un cercle.
  • Produit scalaire dans l'espace.

 

4. TRANSFORMATIONS PLANES (16 h)

  • Isométrie. Translation.
  • Rotation plane.
  • Réflexion.

 

 

ANALYSE (FONCTIONS NUMERIQUES) (42 h)

1. DEFINITIONS ET REPRESENTATION (14 h)

  • Limite d'une fonction. Asymptotes.
  • Suites numériques. Suites arithmétiques. Suites géométriques.

 

2. CONTINUITE ET DERIVATION (22 h)

  • Continuité.
  • Dérivée d'une fonction en un point.
  • Fonction dérivée.
  • Etude des fonctions: fonctions polynômes, fonctions rationnelles.

 

3. INTEGRATION (6 h)

  • Primitives d'une fonction continue sur un intervalle.

 

 

TRIGONOMETRIE (15 h)

1. LIGNES TRIGONOMETRIQUES (4 h)

  • Angle orienté de deux vecteurs.
  • Formules trigonométriques usuelles.

 

2. EQUATIONS TRIGONOMETRIQUES (7 h)

  • Résolutions des équations de la forme sinx = a, cosx = a, tanx = a.

 

3. FONCTIONS CIRCULAIRES (4 h)

  •  Etude des fonctions circulaires.

 

 

STATISTIQUE ET PROBABILITE (20 h)

1. STATISTIQUE (8 h)

  • Variable continue; répartition en classes.
  • Séries statistiques des effectifs et des fréquences; histogramme, polygones.
  • Séries statistiques des effectifs et des fréquences cumulés; histogramme, polygones.

 

2. PROBABILITE (12 h)

  • Notion de probabilité.
  • L'univers des possibles. Cas d'événements équiprobables.
  • Propriétés de la probabilité.
  • Calcul de probabilités: événement (A et B), événement (A ou B), événements incompatibles, événements contraires.

 
 
3ème Année Secondaire – Série Lettres et Humanites

SYLLABUS

 

ALGEBRE (20 h)

1. FONDEMENTS (10 h)

  • Loi de composition interne.
  • Structure de groupe.
  • Eléments de calcul de propositions.

 

2. EQUATIONS ET INEQUATIONS (10 h)

  • Situations-problèmes se ramenant à la résolution d'équations et d'inéquations.

 

 

ANALYSE (FONCTIONS NUMERIQUES) (25)

1. DEFINITIONS ET REPRESENTATION (15 h)

  • Fonctions rationnelles simples.
  • Lecture graphique.
  • Croissance exponentielle et fonction exponentielle.

 

2. MODELES MATHEMATIQUES POUR L'ECONOMIE ET LES SCIENCES SOCIALES (10 h)

  • Intérêt simple. Intérêt composé.

 

 

STATISTIQUE ET PROBABILITE (15 h)

1. STATISTIQUE (10 h)

  • Caractéristiques de position et de dispersion d'une série statistique à une variable (continue ou discrète).

 

2. PROBABILITE (5 h)

  • Probabilité conditionnelle: définition, indépendance de deux événements.

 
 

 

 
3ème Année Secondaire – Série Sociologie et Economie

SYLLABUS

 

ALGEBRE (25 h)

1.  FONDEMENTS (8 h)

  • Loi de composition interne.
  • Structure de groupe.

 

2.  CALCUL NUMERIQUE ET LITTERAL (7 h)

  • Combinaisons: définition, notation, formule du binôme.

 

3.  EQUATIONS ET INEQUATIONS (10 h)

  • Système d'équations linéaires (m x n): définition, opérations élémentaires sur les lignes, méthode de Gauss.

 

 

ANALYSE (FONCTIONS NUMERIQUES) (60 h)

1.  DEFINITIONS ET REPRESENTATION (20 h)

  • Fonctions rationnelles.
  • Fonction réciproque.
  • Fonction logarithme népérien. Fonction logarithme à base a.
  • Fonctions exponentielles.
  • Suites numériques. Suites géométriques: limites.

 

2.  CONTINUITE ET DERIVATION (5 h)

  • Dérivation des fonctions composées.
  • Dérivée seconde.
  • Règle de l'Hôpital.

 

3.  INTEGRATION (10 h)

  • Intégrale: définition, propriétés, calcul.

 

4.  EQUATIONS DIFFERENTIELLES (10 h)

  • Définition.
  • Equations à variables séparables.
  • Equations linéaires du premier ordre à coefficients constants.
  • Equations aux différences finies.

 

5.  MODELES MATHEMATIQUES POUR L'ECONOMIE ET LES SCIENCES SOCIALES (15 h)

  • Fonctions de l'économie et des sciences sociales.
  • Mathématiques financières.

 

 

STATISTIQUE ET PROBABILITE (35 h)

1.  STATISTIQUE (15 h)

  • Caractéristiques de position et de dispersion d'une série statistique à une variable (continue ou discrète).
  • Série statistique à deux variables: introduction, nuage de points, point moyen.
  • Covariance de deux variables, coefficient de corrélation linéaire.
  • Ajustement linéaire et droit de régression.

 

2.  PROBABILITE (20 h)

  • Probabilité conditionnelle: définition, indépendance de deux événements.
  • Formule des probabilités totales.
  • Variable aléatoire réelle, loi de probabilité associée, fonction de répartition. Caractéristiques.

 

 
 

 

 
3ème Année Secondaire – Série Sciences Générales

SYLLABUS

 

ALGEBRE (60 h)

1. FONDEMENTS (15 h)

  • Loi de composition interne.
  • Structure de groupe.
  • Eléments de calcul de propositions.

 

2. CALCUL NUMERIQUE ET LITTERAL (10 h)

  • Combinaisons: définition, notation, formule du binôme, triangle de Pascal.

 

3. EQUATIONS ET INEQUATIONS (10 h)

  • Système d'équations linéaires (m x n): définition, opérations élémentaires sur les lignes, Méthode de Gauss.
  • Equation du second degré à coefficients complexes.

 

4. NOMBRES (25 h)

  • Module et argument d'un nombre complexe. Propriétés.
  • Formes trigonométrique et exponentielle d'un nombre complexe.
  • Interprétation géométrique de l'addition, de la multiplication des nombres complexes et du passage au conjugué.
  • Formule de Moivre. Applications.
  • Racines nème d'un nombre complexe, représentation géométrique des racines nème de l'unité.
  • Interprétation géométrique de  et de  
  • Application.

 

 

GEOMETRIE (90 h)

1. ETUDE CLASSIQUE (20 h)

  • Coniques: définition, foyers, directrice, excentricité, axe focal.
  • Equation d'une conique, sommets, centre, éléments de symétrie, équation réduite.
  • Courbes du second degré.

 

2. ETUDE VECTORIELLE (5 h)

  • Lignes de niveau
  • Equation vectorielle d'une droite, d'un plan, d'une sphère.

 

3. ETUDE ANALYTIQUE (30 h)

  • Composantes du produit vectoriel. Produit mixte.         
  • Equation d'un plan et d'une droite dans l'espace.
  • Orthogonalité de deux droites, d'une droite et d'un plan; plans perpendiculaires.
  • Parallélisme des droites et des plans.
  • Distance d'un point à un plan, à une droite.
  • Equation d'une sphère.
  • Intersection d'une sphère avec une droite, un plan ou une sphère.

 

4. TRANSFORMATIONS PLANES (35 h)

  • Déplacements dans le plan.
  • Homothétie.
  • Forme complexe d'une transformation plane.
  • Similitudes planes directes: définition, forme complexe.
  • Transformations définies par f(z) = az + b ou

 

 

ANALYSE (FONCTIONS NUMERIQUES) (105 h)

1. DEFINITIONS ET REPRESENTATION (40 h)

  • Fonctions irrationnelles (cas simples).
  • Fonction réciproque.
  • Fonctions trigonométriques inverses.
  • Fonction logarithme népérien. Fonction logarithme à base a.
  • Fonctions exponentielles. Fonctions puissances.
  • Suites numériques: limites, suites bornées, suites convergentes.
  • Courbes paramétrées.

 

2. CONTINUITE ET DERIVATION (25 h)

  • Image d'un intervalle fermé par une fonction continue.
  • Prolongement par continuité d'une fonction.
  • Dérivation des fonctions composées.
  • Dérivée d'une fonction réciproque.
  • Dérivée seconde. Dérivées successives.
  • Théorème de Rolle. Egalité et inégalités des accroissements finis. Règle de l'Hôpital.

 

3. INTEGRATION (30 h)

  • Intégrale: définition, propriétés.
  • Méthodes d'intégration.
  • Théorème de la moyenne. Inégalités de la moyenne.
  • Applications du calcul intégral.

 

4. EQUATIONS DIFFERENTIELLES (10 h)

  • Définition.
  • Equations à variables séparables.
  • Equations linéaires du premier ordre à coefficients constants.
  • Equations linéaires du second ordre à coefficients constants.

 

 

TRIGONOMETRIE (15 h)

1. LIGNES TRIGONOMETRIQUES (5 h)

  • Relations métriques dans un triangle. Calcul d'aires.

 

2. EQUATIONS TRIGONOMETRIQUES (5 h)

  •  Résolution d'équations trigonométriques simples.

 

3. FONCTIONS CIRCULAIRES (5 h)

  • Etude des fonctions circulaires de la forme a cos (bx + c) et a sin (bx + c).

 

 

STATISTIQUE ET PROBABILITE (30 h)

1. STATISTIQUE (10 h)

  • Caractéristiques de position et de dispersion d'une série statistique à une variable (continue ou discrète).

 

2. PROBABILITE (20 h)

  • Probabilité conditionnelle: définition, indépendance de deux événements.
  • Formule des probabilités totales.
  • Variable aléatoire réelle, loi de probabilité associée, fonction de répartition. Caractéristiques.

 
 
3ème Année Secondaire – Série Sciences de la Vie

SYLLABUS

 

ALGEBRE (35 h)

1. FONDEMENTS (8 h)

  • Loi de composition interne.
  • Structure de groupe.

 

2. CALCUL NUMERIQUE ET LITTERAL (10 h)

  • Combinaisons: définition, notation, formule du binôme, triangle de Pascal.

 

3. EQUATIONS ET INEQUATIONS (7 h)

  • Système d'équations linéaires (m x n): définition, opérations élémentaires sur les lignes, Méthode de Gauss.

 

 

4. NOMBRES (10 h)

  • Module et argument d'un nombre complexe, propriétés.
  • Forme trigonométrique et exponentielle d'un nombre complexe.
  • Interprétation géométrique de l'addition, de la multiplication des nombres complexes et du passage au conjugué.
  • Formule de Moivre, applications.

 

 

GEOMETRIE (15 h)

1. ETUDE ANALYTIQUE (15 h)

  • Composantes du produit vectoriel. Produit mixte.         
  • Equation d'un plan et d'une droite dans l'espace.
  • Orthogonalité de deux droites, d'une droite et d'un plan; plans perpendiculaires.
  • Parallélisme des droites et des plans.
  • Distance d'un point à un plan, à une droite.

 

 

ANALYSE (FONCTIONS NUMERIQUES) (65 h)

1. DEFINITIONS ET REPRESENTATION (25 h)

  • Fonction réciproque.
  • Fonctions trigonométriques inverses.
  • Fonction logarithme népérien. Fonction logarithme à base a.
  • Fonctions exponentielles.

 

2. CONTINUITE ET DERIVATION (15 h)

  • Image d'un intervalle fermé par une fonction continue.
  • Dérivation des fonctions composées.
  • Dérivée d'une fonction réciproque.
  • Dérivée seconde. Dérivées successives.
  • Règle de l'Hôpital.

 

3. INTEGRATION (15 h)

  • Intégrale: définition, propriétés.
  • Méthodes d'intégration.
  • Applications du calcul intégral.

 

 

4. EQUATIONS DIFFERENTIELLES (10 h)

  • Définition.
  • Equations à variables séparables.
  • Equations linéaires du premier ordre à coefficients constants.
  • Equations linéaires du second ordre à coefficients constants.

 

 

 

TRIGONOMETRIE (5 h)

1. FONCTIONS CIRCULAIRES (5 h)

  • Etude des fonctions circulaires de la formea cos (bx + c) et a sin (bx + c).

 

 

STATISTIQUE ET PROBABILITE (30 h)

1. STATISTIQUE (10 h)

  • Caractéristiques de position et de dispersion d'une série statistique à une variable (continue ou discrète).

 

2. PROBABILITE (20 h)

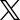
  • Probabilité conditionnelle: définition, indépendance de deux événements.
  • Formule des probabilités totales.
  • Variable aléatoire réelle, loi de probabilité associée, fonction de répartition. Caractéristiques.
  • Variable de Bernoulli.
  • Loi binomiale.